[ad_1]
Framework
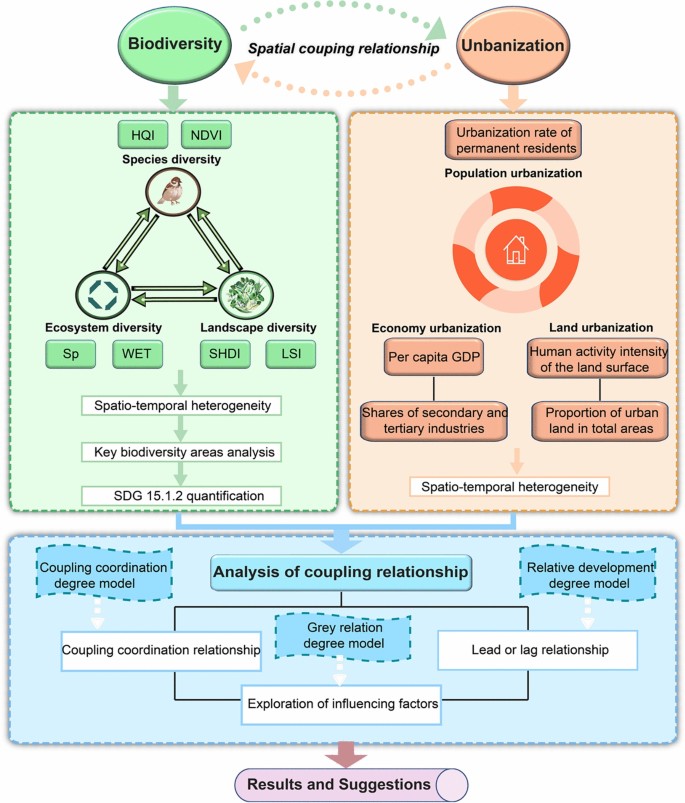
This study was divided into three sections (Fig. 3). In the first part, this study selected six indicators from species, ecosystem, and landscape diversity to construct a remote sensing system based on the InVEST model. Then, the level of biodiversity sustainability was quantified by the proportion of KBAS. In the second part, five indicators were selected from three dimensions to build comprehensive urbanization system based on panel data. In the third part, the coupling coordination relationship between biodiversity and urbanization was quantified based on the CCD model. The lead-lag type was quantified between the two in different developmental processes based on the relative development degree model. Furthermore, the key influencing factors in the coupling coordination system were revealed based on the grey relation model.
Evaluation of biodiversity
Species diversity
HQI
Habitat quality determines the ability of the natural environment to provide for the suitable survival of individuals and sustainable development of the populations. It is positively correlated with biodiversity abundance, and is often used as an important index to assess biodiversity38,39. The habitat quality module of InVEST model can characterize the response degree of different habitats to threat factors and the interactions between threat factors40. HQI has some reference value in areas where species distribution information is poor or where there is a mixture of habitat types coexisting. To a certain extent, HQI is a representation of biodiversity. The calculation process is as follows9,10,40:
$${Q}_{xj}={H}_{j}[1-(\frac{{D}_{xj}^{z}}{{D}_{xj}^{z}+{k}^{z}})]$$
(1)
where \({Q}_{xj}\) is the habitat quality of land type \(j\) in grid cell \(x\), \({H}_{j}\) is the habitat suitability of land type \(j\), \(k\) is half-saturation and constant, and \(z\) is the model default parameter which can be set to 2.5. By referring to the recommended values of the model, current biodiversity situation of the lower Yellow River and related study results41,42, the value of the correlation factor of the threat source are determined. Threat factors of related data in the AYRSP are shown as Table 1, as well as the data of the habitat suitability and the sensitivity of threat factors are shown as Table 2.
$${D}_{xj}=\sum_{r=1}^{R}\sum_{y=1}^{{Y}_{r}}\left(\frac{{w}_{r}}{\sum_{r=1}^{R}{w}_{r}}\right){r}_{y}{i}_{rxy}{\beta }_{x}{S}_{jr}$$
(2)
where \({D}_{xj}\) denotes the habitat degradation degree of grid \(x\) in landscape \(j\), \(R\) is the number of threat factors, \({w}_{r}\) is the weight of threat factor \(r\), \({Y}_{r}\) is the total number of grid cells for threat factor \(r\), \({r}_{y}\) is the intensity of threat factor,\({\beta }_{x}\) represents the anti-interference level of the habitat,\({S}_{jr}\) is the magnitude of sensitivity of the landscape \(j\) to threat factors, \({i}_{rxy}\) means the threat level of threat factor to habitat.
NDVI
NDVI is a vegetation index that not only reflects the photosynthetic activity of vegetation, but also predicts the richness and diversity of species43. Some scholars believe that there is a significant correlation between vegetation indices such as NDVI and plant diversity44. The formulation is as follows:
$$NDVI=({\rho }_{NIR}-{\rho }_{red})/({\rho }_{NIR}+{\rho }_{red})$$
(3)
where \({\rho }_{NIR}, {\rho }_{red}\) represent the reflectance of near-infrared and red bands of Landsat 8 images, respectively.
Ecosystem diversity
WET
WET obtained through the tasseled-cap transformations has been widely used in ecosystem monitoring. WET reflects the moisture in vegetation, water, and soil, which is the basic condition for the reproduction and growth of organisms, and also reflects the richness of biodiversity in an ecosystem to a certain extent45. The larger the WET is, the more suitable it is for the survival and reproduction of species. It is as shown:
$$WET=0.1511{b}_{2}+0.1973{b}_{3}+0.3283{b}_{4}+0.3407{b}_{5}-0.7117{b}_{6}-0.4459{b}_{7}$$
(4)
where \({b}_{2}\)–\({b}_{7}\) represent the reflectance of bands 2–7 of Landsat 8 /OLI data, respectively.
\({S}_{p}\)
Since the nineteenth century, scientists have recognized the relationship between the number of species and the habitat area. Later, Fu et al.46 pointed out that the habitat patch area not only affects the number of species, but also affects the productivity level and the distribution of energy and nutrients in the ecosystem. Theoretically, there is a positive correlation between habitat area and biological species, and species richness is also correlated with ecosystem type. Therefore, \({S}_{p}\) can better characterize the structure and type of ecosystem. In addition, some studies13,18,47 have used \({S}_{p}\) as a measure of ecosystem diversity to evaluate biodiversity. \({S}_{p}\) is calculated as follows:
$${S}_{p}=\frac{{A}_{e}}{{A}_{l}}$$
(5)
where \({S}_{p}\) denotes the percentage of habitat area; \({A}_{e}\) is the habitat area including forest, grassland, garden, and water body; \({A}_{l}\) is the total ecosystem area.
Landscape diversity
SHDI
SHDI focuses on the diversity of patch types, and can accurately capture the uneven distribution of patch types in the landscape. The higher the degree of landscape fragmentation, the higher the SHDI, and the richer the regional biodiversity18,20,21. SHDI is calculated as follows:
$$SHDI=-\sum_{i=1}^{m}{P}_{i}\text{ln}({P}_{i})$$
(6)
where \(m\) is the number of landscape types,\({P}_{i}\) is the proportion of area occupied by landscape type \(i\).
LSI
LSI focuses on the complexity of patch shape in the landscape, and can comprehensively reflect the shape heterogeneity and connectivity of the landscape. Some studies have found that LSI is significantly positively correlated with regional biodiversity48. The larger the LSI, the higher the complexity of the overall distribution of each landscape, and the richer the biodiversity. LSI is calculated by the following formula:
$$LSI=\frac{0.25E}{\sqrt{A}}$$
(7)
where \(E\) is the total length of all patch boundaries in the landscape, A is the total area of the landscape.
Construction of biodiversity indicator
The above indicators are positive, so the standardized calculation is as follows:
$$X_{ij}^{\prime } = \frac{{X_{ij} – min \left\{ {X_{ij} } \right\}}}{{max \left\{ {X_{ij} } \right\} – min \left\{ {X_{ij} } \right\}}}$$
(8)
where \({X}_{ij}^{\prime}\) is the value of the evaluation indicator after normalization, \({X}_{ij}\) is the value of the evaluation indicator before normalization, \(min\left\{{X}_{ij}\right\}\) is the minimum value in the evaluation indicator before normalization, \(max\left\{{X}_{ij}\right\}\) is the maximum value in the evaluation indicator before normalization.
The analytic hierarchy process (AHP)49 is used to determine the weights. This study made reference to relevant studies10,18,47,50 and fully took into account the influencing factors of biodiversity in the AYRSP to determine the relative importance of indicators. Then, the judgment matrix is constructed, and the eigenvector corresponding to the maximum eigenvalue of the matrix is calculated and normalized to obtain the weight value of each indicator (Table 3). At last, the consistency test is conducted by:
$$CI=\frac{LA-N}{N-1}$$
(9)
$$CR=\frac{CI}{RI}$$
(10)
where \(CI\) is the consistency index, \(LA\) is the maximum eigenvalue of the judgment matrix, \(N\) is the order of the judgment matrix, N = 6; \(CR\) represents the proportion of random consistency, \(RI\) is the average random consistency index. After calculation, CR = 0.06 < 0.1. The judgment matrix passed the consistency test on the whole, so the weight value is reasonable and reliable.
Finally, the biodiversity indicator is calculated as follows:
$$BI=HQI\times {\beta }_{1}+NDVI\times {\beta }_{2}+{S}_{p}\times {\beta }_{3}+WET\times {\beta }_{4}+SHDI\times {\beta }_{5}+LSI\times {\beta }_{6}$$
(11)
where \({\beta }_{i}\) is the weight coefficient corresponding to each index.
Evaluation of sustainable development level of biodiversity
The quantitative assessment of SDG 15.1.2 mainly focuses on the identification and extraction of KBAs to provide support for biodiversity conservation and sustainable development. The 25 counties on the mainstream of the Yellow River in the Shandong province are the core areas in the protection of Yellow River basin. Accordingly, the AYRSP was regarded as a key policy protection area. We referred to the method of Liu et al.10,18 to evaluate the sustainable development level of biodiversity by taking the proportion of KBAs to the land area. SDG 15.1.2 (\({X}_{s}\)) is calculated as follows:
$${X}_{s}=\frac{{A}_{i}}{A}$$
(12)
where \({A}_{i}\) is the area of high-level biodiversity area (BI ≥ 0.6), which is considered as KBAs; A is the area of the core protection areas. In order to facilitate the comparison of the results, the Sustainable Development Solutions Network (SDSN) delimited the classification threshold for each index value (Table 4).
Evaluation of urbanization level
HAILS
Selecting HAILS to represent the development of land urbanization can reflect the comprehensive effects of human, social, and economic activities on land resources. HAILS is calculated based on the construction land equivalent sum of different land use types in the region26.
$${HAILS}_{i}=\frac{{S}_{CLE-i}}{{S}_{i}}\times 100\text{\%}$$
(13)
$${S}_{CLE-i}=\sum_{j=1}^{m}({SL}_{ij}\times {CI}_{ij})$$
(14)
where \({HAILS}_{i}\) is the human activity intensity of the land surface in area \(i\) (%), \({S}_{CLE-i}\) is the equivalent area of construction land in region \(i\), \({S}_{i}\) is the land area of the region \(i\), \({SL}_{ij}\) is the area of the land type \(j\) in the region \(i\), \({CI}_{ij}\) is the construction land coefficient discounted for the land type \(j\) in the region \(i\), \(m\) is the number of land types in the region \(i\).
Construction of comprehensive urbanization indicator
This study selected the per capita GDP, shares of secondary and tertiary industries, urbanization rate of permanent residents, proportion of built-up areas in total areas, and HAILS from three dimensions to construct an urbanization indicator system using entropy method (Table 5). Additionally, it is necessary to standardize the indicators before constructing the indicator system. The calculation process of urbanization indicators is as follows29:
$${P}_{ikj}={y}_{ikj}/{\sum }_{i=1}^{m}{\sum }_{k=1}^{n}{y}_{ikj}$$
(15)
$${e}_{j}=-\frac{1}{\text{ln}(m\times n)}{\sum }_{i=1}^{m}{\sum }_{k=1}^{n}{P}_{ikj}ln{P}_{ikj}$$
(16)
$${W}_{j}=\frac{1-{e}_{j}}{n-{\sum }_{j=1}^{z}{e}_{j}}$$
(17)
$$UI=\sum_{j=1}^{z}{W}_{j}{Y}_{ij}$$
(18)
where \({P}_{ikj}\) is the proportion of the indicator \(j\) of the county \(k\) in year \(i\), \({e}_{j}\) is the entropy value of indicator \(j\), \({W}_{j}\) is the weight of the indicator \(j\) in urbanization indicator system, \({Y}_{ij}\) is the normalized value of the indicator \(j\) in the region \(i\) in this system, \(z\) is the number of indicators in this system.
Analysis of the coupling relationship between biodiversity and urbanization
Coupling coordination degree model
CCD model is used to evaluate the relationship between biodiversity and urbanization of the 25 counties in the AYRSP.
$$C=2\sqrt{\frac{B\times U}{{(B+U)}^{2}}}$$
(19)
$$D=\sqrt{C\times T}$$
(21)
where \(C\) represents the coupling degree between biodiversity and urbanization level, \(B\) is the evaluation value of BI, \(U\) is the evaluation value of UI, \(T\) is the evaluation value of BI and UI, \(D\) is the coupling coordination degree, which is in the range of [0, 1]. Two systems are of equal importance, thus, a = b = 0.5. Referring to some studies29,31, the classification of CCD is shown in Table 6.
Relative development degree model
In order to further determine the lead or lag relationship between urbanization and biodiversity on the county scale, the study calculated their relative development degree. Based on the results of other studies29,31, the relative development types are categorized as follows (Table 7).
Grey relation degree model
In order to study the influencing factors of coupling coordination development between biodiversity and urbanization on the county scale, the grey relation model is used to measure the correlation degree of the indicators in two systems to the coupling coordination degree. This study took the sequence of the coupling coordination degree between biodiversity and urbanization as the reference sequence, and took each indicator’s value of two systems as the comparison sequence. The formula is as follows35:
$${\xi }_{i}(k)=\frac{\underset{i}{\text{min}}\underset{k}{\text{min}}\left|{x}_{0}\left(k\right)-{x}_{i}\left(k\right)\right|+\rho \cdot \underset{i}{\text{max}}\underset{k}{\text{max}}|{x}_{0}\left(k\right)-{x}_{i}\left(k\right)|}{\left|{x}_{0}\left(k\right)-{x}_{i}\left(k\right)\right|+\rho \cdot \underset{i}{\text{max}}\underset{k}{\text{max}}|{x}_{0}\left(k\right)-{x}_{i}\left(k\right)|}$$
(22)
$${\xi }_{i}=\frac{1}{n}\sum_{k=1}^{n}{\xi }_{i}(k)$$
(23)
where \({\xi }_{i}(k)\) represents the grey relation coefficients between the degree of coupling coordination and the indicators of the two systems in year \(k\); \({x}_{0}\left(k\right)\) is the normalized value of the coupling coordination degree of two systems in the year \(k\); \({x}_{i}\left(k\right)\) is the normalized value of the internal indicators of two systems in year \(k\) (\(i\)=1,2…,7); ρ denotes the coefficient of variation, which usually takes the value of 0.5; \(n\)=4; \({\xi }_{i}\) represents the grey relation degree between the coupling coordination degree and the influencing indicators of two systems. The more \({\xi }_{i}\) tends to 1, indicating that the greater the influence of the indicator on the coupling coordination degree. Referring to the related research35, the classification of the grey relation degree is shown as Table 8.
[ad_2]
Source link